

时间: 2023-12-01 文章来源: 洋蜜蜂Online Tutor
上个章节洋蜜蜂小编跟大家分享了中心极限定理(Central Limit Theorem,CLT)的概念及在及在各行业领域的应用,以及其对金融分析提供的帮助。本章我们将介绍的是贝叶斯定理(Bayes' Theorem)。

留学生统计学系列—chap.5贝叶斯定理(Bayes' Theorem)
贝叶斯定理是一种统计学原理,用于计算条件概率,即在已知一些信息的情况下,计算另一事件发生的概率。它由英国统计学家托马斯·贝叶斯(Thomas Bayes)首次提出,后来由皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)进一步发展和推广。贝叶斯定理在概率论和统计学中被广泛应用,尤其在机器学习、人工智能、数据分析和决策支持系统中具有重要地位。
贝叶斯定理的一般形式如下:
P(A|B) = (P(B|A) * P(A)) / P(B)
其中:
P(A|B) 表示在事件 B 已经发生的条件下,事件 A 发生的概率,这被称为后验概率。
P(B|A) 表示在事件 A 已经发生的条件下,事件 B 发生的概率,这被称为似然。
P(A) 和 P(B) 分别是事件 A 和事件 B 单独发生的概率,分别被称为先验概率。
贝叶斯定理允许我们根据先验概率和新的证据(似然)来更新我们对事件的概率估计,从而得到更准确的后验概率。贝叶斯定理是由18世纪英国统计学家托马斯·贝叶斯(Thomas Bayes)首次提出的。他的思想和工作主要集中在概率论和统计学领域,尽管他的许多著作在他去世后才被发现,但其中包含了贝叶斯定理的基本思想。
贝叶斯定理的发现过程可以追溯到贝叶斯的一封信,这封信于1763年写给皮埃尔-西蒙·拉普拉斯的,但直到1764年贝叶斯去世后,这封信才被发现。在这封信中,贝叶斯讨论了如何使用概率来估计未知事件的概率,尤其是在有限的数据或证据情况下。
贝叶斯定理的核心思想是,我们可以通过结合先验概率和新的证据来更新我们对事件的概率估计。贝叶斯将这一思想应用于关于概率的推断,尤其是在掷硬币或其他随机事件的情况下。虽然他没有详细提供定理的数学形式,但他的思想为后来的统计学家提供了重要的启发。
皮埃尔-西蒙·拉普拉斯在18世纪末和19世纪初对贝叶斯思想进行了拓展和形式化,将其发展为今天所知的贝叶斯定理的数学形式。拉普拉斯的工作使贝叶斯定理在统计学和概率论中得到广泛应用,成为了一种强大的工具,用于概率推断、数据分析和决策支持系统。所以,尽管贝叶斯定理是由托马斯·贝叶斯首次提出的,但它的形式化和广泛应用主要得益于后来的统计学家和数学家的工作,特别是拉普拉斯。
贝叶斯定理在现代有广泛的应用,尤其是在以下领域:
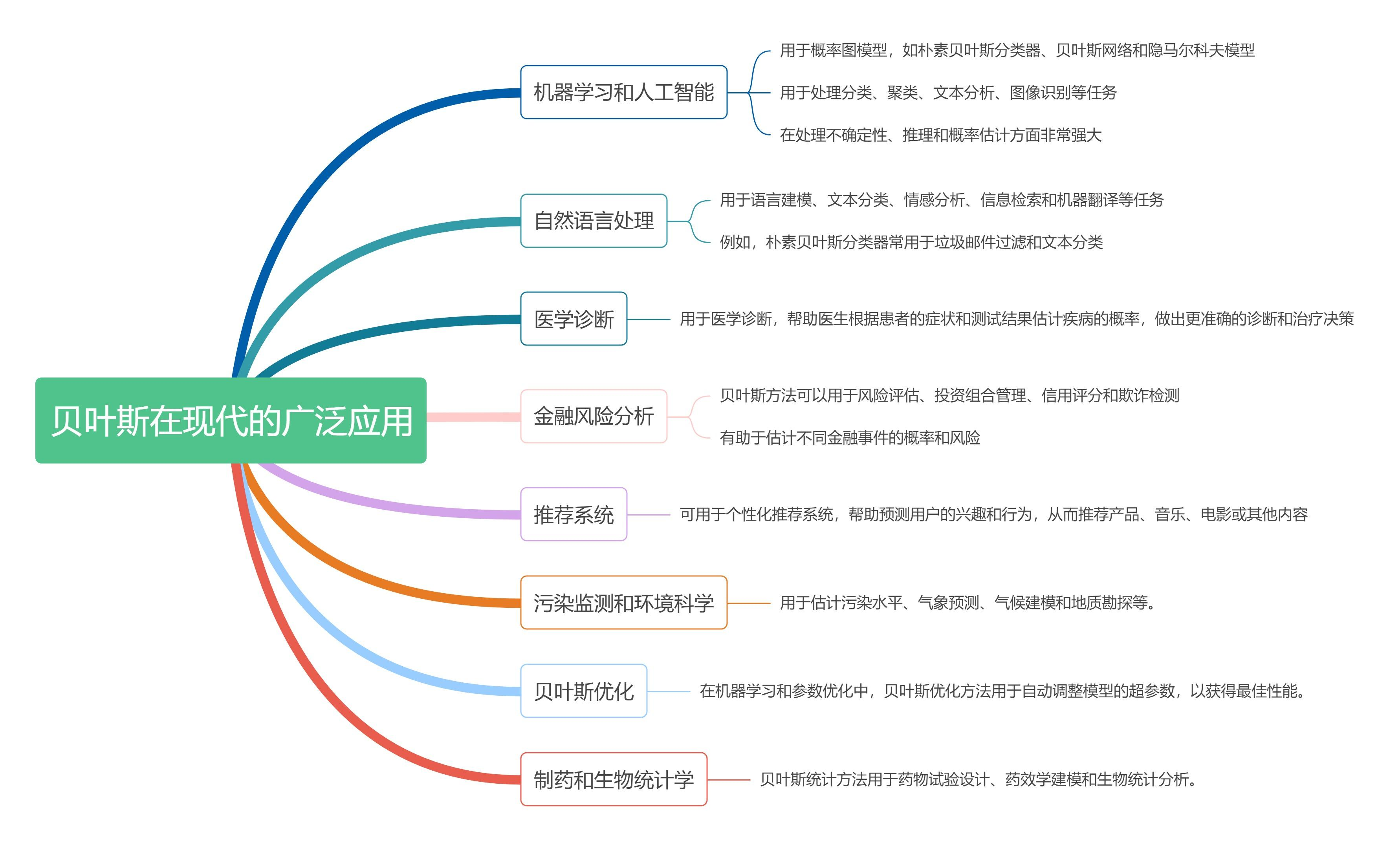
留学生统计学系列—chap.5贝叶斯定理(Bayes' Theorem)
这些只是贝叶斯定理在现代应用的一些示例。其强大的概率推断和不确定性建模能力使其在各种领域都发挥重要作用,帮助人们更好地理解数据、做出决策和预测未来事件。
贝叶斯定理在金融风险分析中可以用于估计不同金融事件的概率和风险,帮助金融机构和投资者更好地理解和管理风险。以下是一些具体的应用和方法:

留学生统计学系列—chap.5贝叶斯定理(Bayes' Theorem)
这里介绍一下在金融风险分析中应用贝叶斯定理通常会需要一些什么步骤:
建立贝叶斯模型
首先,确定要分析的金融事件,并构建一个适当的概率模型,包括先验概率和似然函数。先验概率是在没有新信息之前的事件概率,似然函数是已有的数据对事件的影响。
收集数据
收集与所分析事件相关的数据,包括历史数据、市场数据、财务报表等。这些数据将用于更新先验概率,以获得后验概率。
贝叶斯更新
使用贝叶斯定理将先验概率与新的数据相结合,计算后验概率。这可以通过贝叶斯公式来完成,其中后验概率等于先验概率乘以似然函数,再除以边际似然函数。
风险评估
分析后验概率,以了解事件的风险程度。这可以包括计算风险度量、价值-at-risk(VaR)、条件概率等,以便更好地了解风险和制定决策。
模型验证和更新
定期验证贝叶斯模型的性能,并根据新数据和新信息更新模型,以保持其准确性和适用性。
贝叶斯方法在金融风险分析中能够提供更准确的风险估计和更好的决策支持,特别是在处理不确定性和复杂金融事件时。
建立贝叶斯模型通常涉及以下步骤:
1. 确定问题和目标
首先,明确定义您的问题和分析的目标。了解您要研究的事件或现象是什么,以及您希望通过贝叶斯分析获得什么类型的信息。
2. 选择先验分布
确定事件的先验概率分布,即在考虑任何数据之前的初始信念。先验分布可以基于领域知识、历史数据、专家意见或其他信息来选择。它可以是离散的或连续的,取决于问题的性质。
3. 采集数据
收集与问题相关的数据。这些数据将用于更新您的模型,并计算似然函数。确保数据质量和可靠性对于贝叶斯分析非常重要。
4. 建立似然函数
似然函数描述了数据与参数之间的关系。它表示在给定参数下观察到数据的概率。似然函数的形式取决于具体问题,可以是正态分布、泊松分布、二项分布或其他分布,或者可以是一个自定义的函数。
5. 应用贝叶斯定理
使用贝叶斯定理将先验分布和似然函数相结合,计算后验分布。贝叶斯定理的一般形式如下:
后验分布 ∝ 先验分布 x 似然函数
这里,“∝”表示“正比于”,即后验分布正比于先验分布和似然函数的乘积。
6. 计算后验分布
根据数据和模型参数计算后验分布。这可以通过数值方法(如马尔可夫链蒙特卡洛法)或分析方法(如果模型具有解析解)来完成。
7. 分析后验分布
一旦计算得到后验分布,可以进行分析以获得关于参数或事件的有用信息。这可以包括计算点估计值、置信区间、模型比较等。
8. 模型验证
验证模型的性能,并根据需要进行模型改进和调整。这可以包括模型的适应性检验、模型比较、残差分析等。
9. 应用模型
使用构建的贝叶斯模型来回答您的问题、做出决策或进行预测。这可以涉及将模型集成到决策支持系统中,以帮助解决特定问题。
10. 持续更新
定期更新模型,以反映新的数据和信息,确保模型的准确性和实用性。
建立贝叶斯模型需要充分了解问题领域、数据分析和统计方法。在实际应用中,通常需要使用统计分析软件和编程语言(如Python或R)来进行模型构建和分析。此外,一些问题可能需要专业的统计学家或数据科学家来进行建模和分析。
以上就是本章小编要分享的内容,贝叶斯定理(Bayes' Theorem)的概念及在各行业领域的应用,以及在金融分析中的具体应用。下个章节小编将介绍的是假设检验(Hypothesis Testing)及其应用。
如果你是统计学专业的留学生或者对统计学感兴趣的准留学生,欢迎关注收藏,如果你在学业上遇到问题,可以试试洋蜜蜂辅导。我们提供优质的老师为你1v1辅导,提供专业留学辅导:数学Mathematics、物理physics、化学chemistry、生物biological sciences、地球科学earth scaiences、计算机科学computer sciences、医学medicine、工程学Engineering、会计Accounting、统计学statistics、精算科学Actuarial Science等涵盖大学90%以上科目。