

时间: 2023-11-29 文章来源: 洋蜜蜂Online Tutor
上个章节洋蜜蜂小编跟大家分享了大数定律(Law of Large Numbers)的概念及在各行业领域的应用,特别是在保险公司的具体应用。本章我们将介绍的是中心极限定理(Central Limit Theorem)。
中心极限定理(Central Limit Theorem,CLT)是统计学中的一个重要原理,描述了当从总体中抽取大量独立同分布的随机样本,并计算这些样本的平均值(或总和)时,这些平均值的分布会趋向于正态分布,无论总体分布是什么。中心极限定理是统计学中最基本的原理之一,具有广泛的应用。
中心极限定理的关键要点包括:
独立同分布样本
CLT要求从总体中抽取的样本必须是独立同分布的,这意味着每个样本在统计上应该相互独立,且具有相同的分布特性。
大样本
CLT通常在样本大小足够大的情况下成立。虽然没有一个明确定义的“大”样本大小,但通常来说,样本大小应该足够大,以便中心极限定理的逼近近似成立。通常,样本大小大于30被认为足够大。
正态分布趋势
根据中心极限定理,当我们重复抽取大量样本并计算它们的平均值(或总和)时,这些平均值将近似地遵循正态分布。这意味着这些平均值的分布将以总体均值为中心,并具有标准差,随着样本大小的增加,这种近似将更加准确。
中心极限定理的重要性在于它提供了一种在实际应用中进行统计推断的方法。无论总体的分布形状如何,只要样本足够大,我们都可以使用正态分布的性质来进行假设检验、置信区间估计和统计推断。这使得中心极限定理在各种领域,包括调查研究、质量控制、金融分析等方面具有广泛的应用。中心极限定理也为许多统计方法的有效性提供了理论基础。
中心极限定理(Central Limit Theorem,CLT)的发展历程可以追溯到18世纪,经历了多个数学家的贡献和进一步的研究。以下是中心极限定理的主要发展历程:
Abraham de Moivre(1718)
英国法国数学家亚伯拉罕·德·莫瓦尔(Abraham de Moivre)是中心极限定理发展的早期贡献者之一。他在1718年的著作《The Doctrine of Chances》中提出了一个特殊情况的中心极限定理,即二项分布的正态近似。
Pierre-Simon Laplace(1810)
法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)进一步推广了中心极限定理的应用,并提出了更一般的版本,适用于不仅仅是二项分布,还适用于更广泛的分布。
Carl Friedrich Gauss(1809)
德国数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss)的工作在正态分布的理论和应用中发挥了重要作用。他研究了正态分布的性质,并为统计学的发展提供了坚实的数学基础。
Augustin-Louis Cauchy(1820)
法国数学家奥古斯丁·路易·柯西(Augustin-Louis Cauchy)的研究进一步完善了中心极限定理的数学证明。
Andrey Kolmogorov(1930s)
俄罗斯数学家安德雷·科尔莫哥洛夫(Andrey Kolmogorov)在20世纪初提出了现代中心极限定理的精确证明,他的工作对统计学和概率论领域产生了深远影响。
总的来说,中心极限定理的发展经历了几个世纪,数学家们不断完善和推广这一理论。中心极限定理的主要思想是,随着样本大小的增加,独立同分布随机变量的和或平均值将近似地遵循正态分布。这一定理为统计学和概率论提供了重要的理论基础,使统计学家能够在各种应用中有效地使用正态分布的性质。它也被认为是统计学中最重要的原理之一。
中心极限定理(Central Limit Theorem,CLT)在现代统计学和数据分析中具有广泛的应用。它的核心思想是,当从总体中抽取大量独立同分布的样本,并计算这些样本的平均值(或总和)时,这些平均值的分布趋向于正态分布。以下是中心极限定理在现代应用中的一些重要领域:
假设检验和置信区间估计
中心极限定理为假设检验和置信区间估计提供了重要的理论基础。无论总体的分布形状如何,统计学家可以使用正态分布的性质来进行参数估计和假设检验,从而得出关于总体参数的统计推断。
质量控制
在制造业和质量控制领域,中心极限定理用于分析产品质量数据。例如,它可以帮助确定产品的平均值和标准差,以确保产品质量符合规定的标准。
金融分析
中心极限定理在金融分析中扮演着关键角色。金融市场中的价格和收益率变化通常可以近似为正态分布,这对风险管理、资产定价和投资组合优化非常重要。
医学研究
在医学研究中,中心极限定理用于分析患者数据,如临床试验结果和流行病学数据。它可以帮助研究人员进行统计推断,评估治疗效果和确定疾病发生率。
调查研究
中心极限定理对民意调查和市场研究有重要影响。研究人员可以使用该定理来估计总体参数,计算置信区间,并确保调查结果的可靠性。
机器学习
在机器学习中,中心极限定理为交叉验证和自助法(bootstrap)等技术提供了支持。这些方法通常要求对数据进行多次抽样和分析,而中心极限定理可以用来解释为什么这些方法有效。
总的来说,中心极限定理为统计学家和数据分析师提供了一种强大的工具,使他们能够在各种应用中进行参数估计、假设检验和数据分析。无论研究的领域是什么,只要满足中心极限定理的基本假设,就可以应用这一原理。这使得中心极限定理成为现代统计学和数据科学的核心概念之一。
中心极限定理(Central Limit Theorem,CLT)在金融分析中具有广泛的应用。
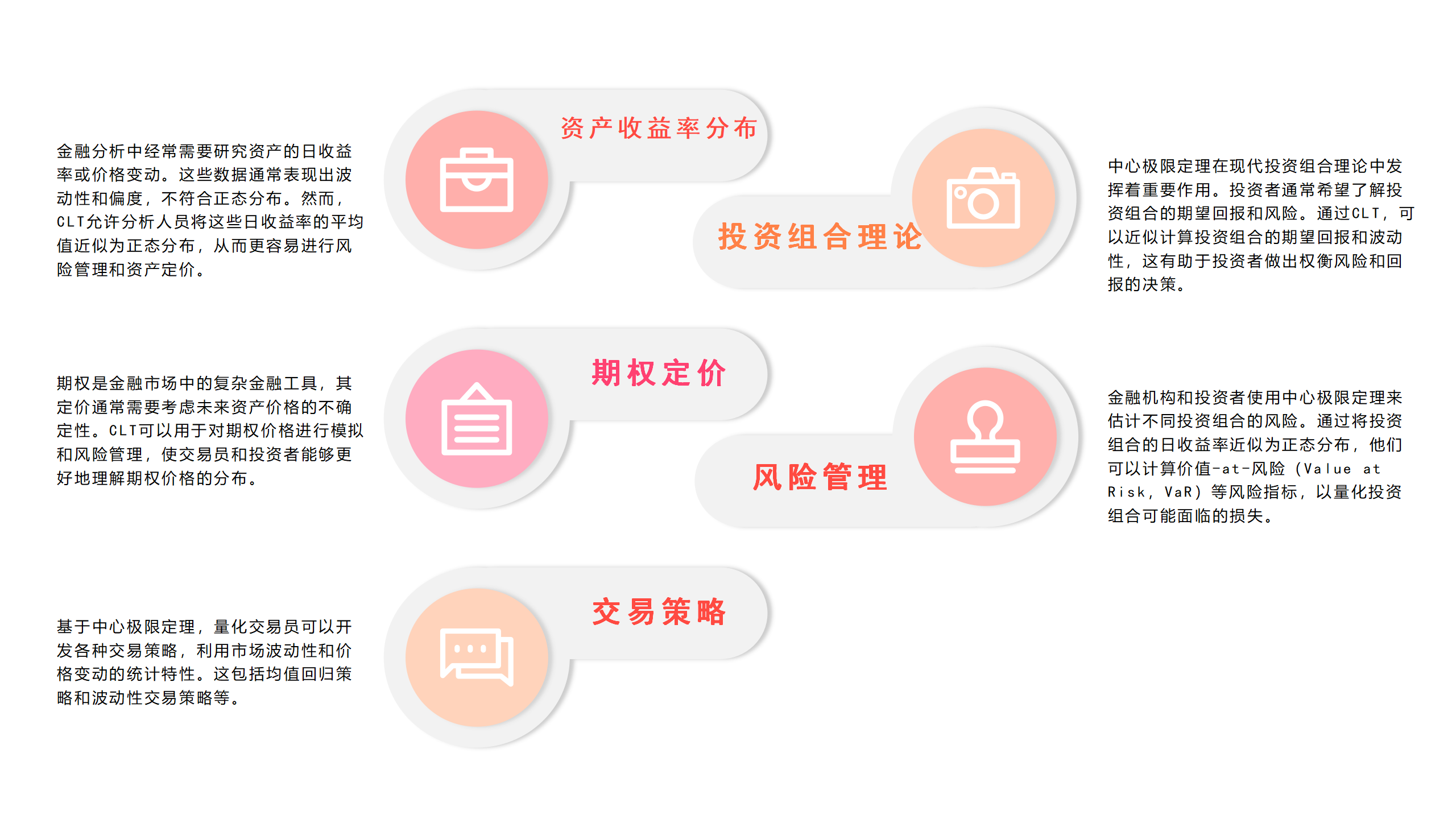
它的核心思想是,无论原始数据的分布如何,当从总体中抽取大量独立同分布的样本并计算这些样本的平均值时,这些平均值的分布趋向于正态分布。这一性质对金融分析非常有用,因为金融数据通常不符合正态分布,但可以通过中心极限定理进行近似处理。以下是中心极限定理在金融分析中的应用:
留学生统计学系列—chap.4中心极限定理(Central Limit Theorem)
中心极限定理为金融分析提供了一个强大的工具,使分析人员能够处理不同分布的金融数据,并进行风险管理、资产定价和投资决策。虽然金融数据通常具有复杂的性质,但中心极限定理允许将它们近似为正态分布,从而简化了分析过程。这使得金融专业人员能够更好地理解市场,管理风险和制定战略。
以上就是本章小编要分享的内容:中心极限定理(Central Limit Theorem,CLT)的概念及在各行业领域的应用,以及其对金融分析提供的帮助。下个章节小编将介绍的是中心极限定理(Central Limit Theorem)及其应用。如果你在学业上遇到问题,可以试试洋蜜蜂辅导。我们提供优质的老师为你1v1辅导,提供专业留学辅导:数学Mathematics、物理physics、化学chemistry、生物biological sciences、地球科学earth scaiences、计算机科学computer sciences、医学medicine、工程学Engineering、会计Accounting、统计学statistics、精算科学Actuarial Science等涵盖大学90%以上科目。