

时间: 2023-12-13 文章来源: 洋蜜蜂Online Tutor
上个章节洋蜜蜂小编跟大家分享了统计学的线性回归(Linear Regression)的发展历史及其应用。本章我们将介绍的是方差分析(Analysis of Variance,ANOVA)的发展历史及其应用。

留学生统计学系列—chap.8方差分析(Analysis of Variance,ANOVA)
方差分析(Analysis of Variance,简称ANOVA)是一种统计方法,用于比较两个或多个组之间的平均值是否存在显著差异。它是一种广泛用于研究实验设计和数据分析的工具,通常用于以下情况:
1. 比较多个组的均值
方差分析用于确定不同组之间的均值是否存在显著性差异。这些组可以是不同的处理组、实验条件、群体或任何其他分组。
2. 检验因素的影响
它可用于确定一个或多个自变量(因素)对因变量(响应变量)的影响是否显著,或者它们是否以某种方式相互作用。
3. 解释变异性
方差分析帮助分析数据中的变异性,将总方差分解为组内方差和组间方差,从而更好地理解数据的结构。
方差分析的基本思想是比较不同组之间的变异性,以确定组内变异性是否与组间变异性相比显著小。如果组间变异性显著大于组内变异性,那么就可以得出结论,不同组之间存在显著差异。
方差分析有几种不同的类型,其中包括:
1. 单因素方差分析
用于比较一个因素(自变量)对一个因变量的影响。例如,比较不同药物剂量对患者疾病症状的影响。
2. 双因素方差分析
用于比较两个因素(自变量)对一个因变量的影响,以检验它们是否以某种方式相互作用。例如,比较不同肥胖水平和性别对心血管疾病风险的影响。
3. 多因素方差分析
用于比较多个因素对一个因变量的影响。它可以用于研究多个自变量对某一现象的复杂影响。
方差分析通常伴随着假设检验,以确定差异是否显著。如果差异是显著的,方差分析还可以进行事后多重比较,以确定哪些组之间存在具体的差异。这有助于科研、实验和决策过程中的统计推断和结论。
方差分析(Analysis of Variance,ANOVA)的发展历史可以追溯到20世纪初,它是统计学领域的一个重要方法,经历了多位统计学家和研究人员的贡献和改进。
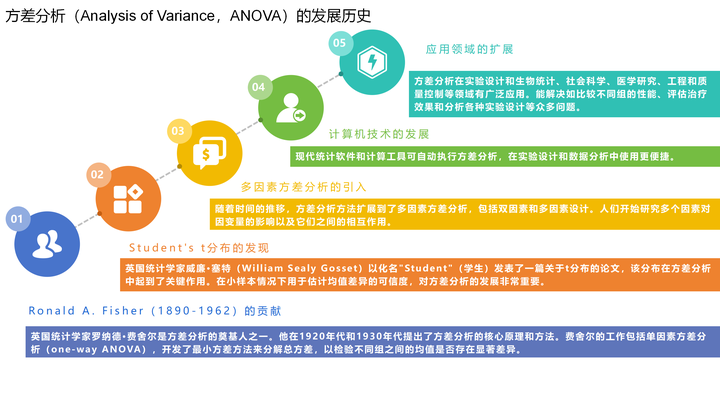
留学生统计学系列—chap.8方差分析(Analysis of Variance,ANOVA)
方差分析是统计学中的一个重要工具,它的发展历史经历了多位著名统计学家的贡献,以及计算机技术的进步。它继续在各种领域中发挥作用,帮助研究人员和决策者进行数据分析和做出推断。
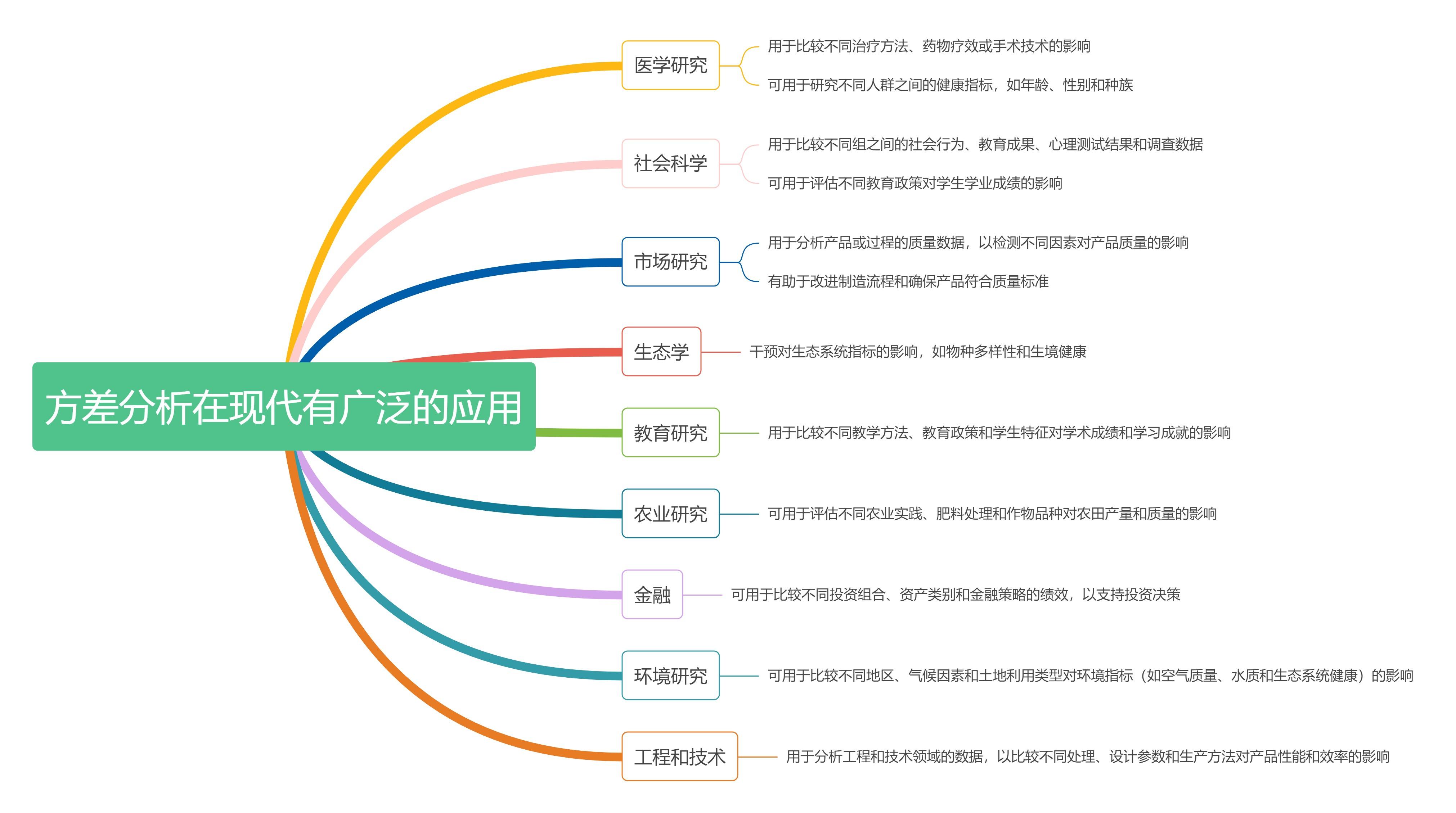
留学生统计学系列—chap.8方差分析(Analysis of Variance,ANOVA)
方差分析在现代有广泛的应用,它不仅限于传统的实验设计领域,还在各种领域中用于比较和分析多组数据之间的差异。
方差分析在环境研究中有多种具体应用,帮助科学家和研究人员分析和比较不同环境因素对生态系统、环境质量和自然资源的影响。生态系统研究/土壤质量分析/水质研究/空气质量分析/野生动植物生态学/气候研究/环境政策评估/自然资源管理/环境毒理学/生态修复研究。
方差分析在空气质量分析中可以用于比较不同时间、地点或空气质量监测站点之间的空气质量数据,以确定各种因素对空气质量的影响是否显著。以下是大致步骤:
1. 数据收集
收集与空气质量相关的数据,包括不同时间段、地点或监测站点的空气质量指标,如PM2.5浓度、NO2浓度、SO2浓度等。
2. 数据准备
整理和清理数据,处理缺失值、异常值和数据标准化,以确保数据的质量和一致性。
3. 确定因素
确定要比较的不同因素,这些因素可能包括时间(季节、月份、年份)、地点(不同城市或监测站点)或其他可能影响空气质量的因素。
4. 构建方差分析模型
基于选择的因素,构建方差分析模型。例如可以考虑以下模型:
5. 单因素方差分析
用于比较不同时间或地点的空气质量数据。
6. 双因素方差分析
用于同时比较时间和地点对空气质量的影响,以检验它们是否相互作用。
7. 拟合模型
使用方差分析工具拟合模型,估计各因素的效应和交互作用。
8. 假设检验
进行假设检验,评估不同因素对空气质量的影响是否显著。检验模型的假设,包括组间变异性是否显著大于组内变异性。
9. 解释结果
解释方差分析的结果,包括各因素对空气质量的影响,是否存在显著差异,以及不同因素之间是否存在相互作用。
10. 事后多重比较
如果方差分析显示不同因素之间存在显著差异,你可以进行事后多重比较来确定哪些时间、地点或监测站点之间存在具体的差异。
11. 报告和决策
将分析结果用于报告和决策。你可以使用结果来评估空气质量的季节性变化、地理差异、空气污染源的影响等,以制定环保政策或改善空气质量措施。
方差分析可帮助你了解各种因素对空气质量的影响,并确定哪些因素对于改善空气质量最为重要。这种分析有助于科学家、政府机构和环境保护组织更好地理解和管理空气质量问题。
在空气质量分析中,方差分析使用的主要公式是针对单因素(单因子)方差分析,以比较不同组之间的均值差异。以下是单因素方差分析的公式和相关术语:
总平方和(Total Sum of Squares,SST)
总平方和表示了所有观测值与全体观测值均值之间的总变异。它的计算公式如下:
SST = Σ(yij - ȳ)²
其中,yij 代表第 i 组中的第 j 个观测值,ȳ 代表所有观测值的总均值。
组间平方和(Between-Groups Sum of Squares,SSB):组间平方和表示了不同组之间的均值差异导致的变异。它的计算公式如下:
SSB = Σ(ni * (ȳi - ȳ)²)
其中,ni 代表第 i 组的观测值数量,ȳi 代表第 i 组的均值,ȳ 是所有组合的总均值。
组内平方和(Within-Groups Sum of Squares,SSW):组内平方和表示了每组内观测值与该组内的均值之间的变异。它的计算公式如下:
SSW = ΣΣ(yij - ȳi)²
其中,yij 代表第 i 组中的第 j 个观测值,ȳi 代表第 i 组的均值。
自由度(Degrees of Freedom,df):方差分析中涉及到两种自由度,分别是组间自由度(dfB)和组内自由度(dfW)。
组间自由度 dfB = k - 1,其中 k 是组数(因子水平数)。
组内自由度 dfW = N - k,其中 N 是总的观测值数量。
均方(Mean Square,MS):均方是平方和与自由度的比值,用于衡量均值差异的平均大小。均方分为两种,分别是组间均方(MSB)和组内均方(MSW):
组间均方 MSB = SSB / dfB
组内均方 MSW = SSW / dfW
F统计量
F统计量用于检验组间均值差异是否显著。它是组间均方与组内均方的比值,计算公式如下:
F = MSB / MSW
p值
p值表示了F统计量的显著性,用于判断组间均值差异是否显著。通常,如果p值小于显著性水平(通常为0.05),则可以拒绝原假设,表示组间均值差异显著。
方差分析的目标是检验不同组之间的均值差异是否显著。如果F统计量的值较大,而p值较小,就可以得出结论,不同组之间的均值存在显著差异,从而对空气质量分析提供了有力的统计依据。

留学生统计学系列—chap.8方差分析(Analysis of Variance,ANOVA)
以上就是本章小编要分享的内容,方差分析(Analysis of Variance,ANOVA)的发展历史及其相关应用。下个章节小编将介绍的是非参数统计(Nonparametric Statistics)。
如果你是统计学专业的留学生或者对统计学感兴趣的准留学生,欢迎关注收藏。如果你在学业上遇到问题,可以试试洋蜜蜂辅导。我们提供优质的老师为你1v1辅导,提供专业留学辅导:数学Mathematics、物理physics、化学chemistry、生物biological sciences、地球科学earth scaiences、计算机科学computer sciences、医学medicine、工程学Engineering、会计Accounting、统计学statistics、精算科学Actuarial Science等涵盖大学90%以上科目。